Funkce s absolutní hodnotou 1

Absolutní hodnota je matematická operace, která vždy z výrazu ve svislých závorkách udělá výraz s kladným znaménkem. Pokud je výraz vevnitř záporný, tak před sebe dá znaménko mínus, které výraz uvnitř udělá kladným.

Absolutní hodnota jako funkce

Absolutní hodnota ve funkcích komplikuje situaci proto, že na definičním oboru funkce se předpis funkce chová jinak podle toho, jaké znaménko má výraz v absolutní hodnotě. 

Na začátek se budeme zabývat základy, a to funkcí y=|x|. Ve videu si ukážeme, jak se odvodí tento její graf.

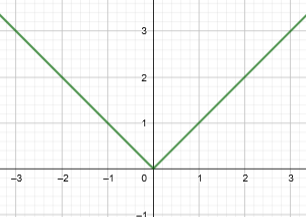
Na tento graf se vztahuje klasická posuvová logika. Pokud přičítáme nebo odčítáme číslo za absolutní hodnotou, tak graf funkce posouváme svisle. Pokud číslo přičítáme nebo odčítáme uvnitř absolutní hodnoty, graf se posouvá vodorovně.

Tento „V“ tvar platí pro funkce s jednou absolutní hodnotou, když  se proměnná nachází pouze v absolutní hodnotě. Zároveň proměnná musí být v první mocnině.

Lineární funkce s absolutní hodnotou

V těchto funkcích již může být několik absolutních hodnot, každopádně všechny proměnné jsou v první mocnině. Např. jako

Postup pro zakreslení těchto funkcí je vždy stejný. Potřebujeme najít nulové body všech absolutních hodnot, protože to jsou hodnoty x, ve kterých se mění hodnoty výrazů v absolutních hodnotách. 

Definiční obor takové funkce je nulovými body rozdělen a v těchto intervalech se funkce chová podle různých předpisů. Jakmile tyto předpisy známe, stačí zakreslit do grafu.

Obrázek vytvořen s použitím softwaru GeoGebra (Created with GeoGebra) - www.geogebra.org